An example of applying mSSA to the coefficients you created using pyEXP
This example assumes that you have run the Part1-Coefficients notebook to create the coefficients.
We begin by importing pyEXP and friends and setting the working directory.
[1]:
import os
import yaml
import math
import pyEXP
import numpy as np
import matplotlib.pyplot as plt
# In this test, I assume that you have already explored and run Part1-Coefficients. This notebook does some additional
# analysis and plotting
#
os.chdir('../Data')
Create the basis
This step is the same as in the previous notebook. We are going to use the basis for field evaluation so we need the basis.
[2]:
# Get the basis config
#
yaml_config = ""
with open('basis.yaml') as f:
config = yaml.load(f, Loader=yaml.FullLoader)
yaml_config = yaml.dump(config)
# Construct the basis instance
#
basis = pyEXP.basis.Basis.factory(yaml_config)
---- SLGridSph::ReadH5Cache: successfully read basis cache <sphereSL.model>
---- Spherical::orthoTest: worst=0.00016446
So far, this is the same as in Part1 … now:
Reading the halo coefficients
We created the halo coefficients in the last notebook and stashed them in the EXP HDF5 format. Now, we’ll read them back.
[3]:
# Reread the coefs from the file
#
coefs = pyEXP.coefs.Coefs.factory('test_coefs')
print("Got coefs for name=", coefs.getName())
Got coefs for name= dark halo
Visualizing the fields
We made a few test grids in Part 1 of the notebook. This time, we’ll make surface renderings:
[4]:
# Now try some slices for rendering
#
times = coefs.Times()
pmin = [-0.05, -0.05, 0.0]
pmax = [ 0.05, 0.05, 0.0]
grid = [ 40, 40, 0]
fields = pyEXP.field.FieldGenerator(times, pmin, pmax, grid)
surfaces = fields.slices(basis, coefs)
print("We now have the following [time field] pairs")
final = 0.0
for v in surfaces:
print('-'*40)
for u in surfaces[v]:
print("{:8.4f} {}".format(v, u))
final = v
# Print the potential image at the final time (I think there is a
# fencepost issue in this grid, no matter).
x = np.linspace(pmin[0], pmax[0], grid[0])
y = np.linspace(pmin[1], pmax[1], grid[1])
xv, yv = np.meshgrid(x, y)
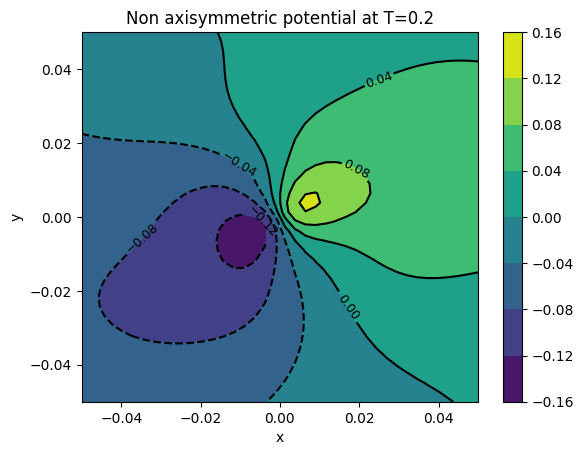
# Visualize the final time slice in grid. Obviously, we could use any
# field we want. Here is potential and radial force.
cont1 = plt.contour(xv, yv, surfaces[final]['potl m>0'], colors='k')
plt.clabel(cont1, fontsize=9, inline=True)
cont2 = plt.contourf(xv, yv, surfaces[final]['potl m>0'])
plt.colorbar(cont2)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Non axisymmetric potential at T={}'.format(final))
plt.show()
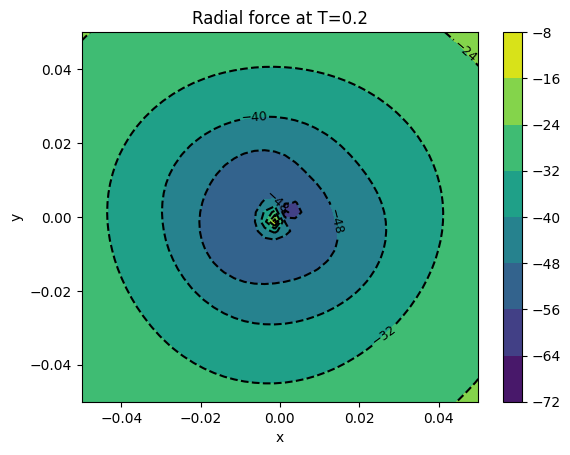
cont1 = plt.contour(xv, yv, surfaces[final]['rad force'], colors='k')
plt.clabel(cont1, fontsize=9, inline=True)
cont2 = plt.contourf(xv, yv, surfaces[final]['rad force'])
plt.colorbar(cont2)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Radial force at T={}'.format(final))
plt.show()
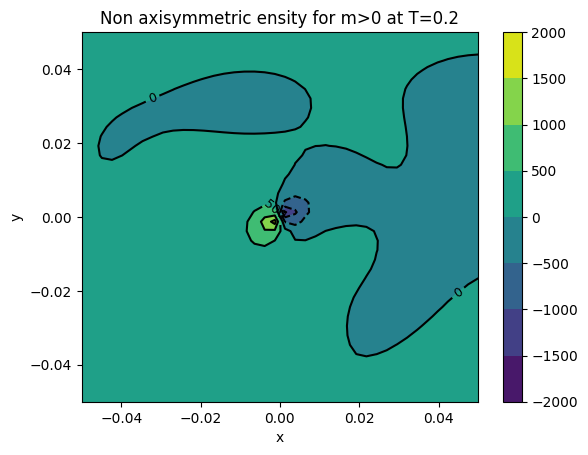
cont1 = plt.contour(xv, yv, surfaces[final]['dens m>0'], colors='k')
plt.clabel(cont1, fontsize=9, inline=True)
cont2 = plt.contourf(xv, yv, surfaces[final]['dens m>0'])
plt.colorbar(cont2)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Non axisymmetric ensity for m>0 at T={}'.format(final))
plt.show()
We now have the following [time field] pairs
----------------------------------------
0.0100 azi force
0.0100 dens
0.0100 dens m=0
0.0100 dens m>0
0.0100 mer force
0.0100 potl
0.0100 potl m=0
0.0100 potl m>0
0.0100 rad force
----------------------------------------
0.0200 azi force
0.0200 dens
0.0200 dens m=0
0.0200 dens m>0
0.0200 mer force
0.0200 potl
0.0200 potl m=0
0.0200 potl m>0
0.0200 rad force
----------------------------------------
0.0300 azi force
0.0300 dens
0.0300 dens m=0
0.0300 dens m>0
0.0300 mer force
0.0300 potl
0.0300 potl m=0
0.0300 potl m>0
0.0300 rad force
----------------------------------------
0.0400 azi force
0.0400 dens
0.0400 dens m=0
0.0400 dens m>0
0.0400 mer force
0.0400 potl
0.0400 potl m=0
0.0400 potl m>0
0.0400 rad force
----------------------------------------
0.0500 azi force
0.0500 dens
0.0500 dens m=0
0.0500 dens m>0
0.0500 mer force
0.0500 potl
0.0500 potl m=0
0.0500 potl m>0
0.0500 rad force
----------------------------------------
0.0600 azi force
0.0600 dens
0.0600 dens m=0
0.0600 dens m>0
0.0600 mer force
0.0600 potl
0.0600 potl m=0
0.0600 potl m>0
0.0600 rad force
----------------------------------------
0.0700 azi force
0.0700 dens
0.0700 dens m=0
0.0700 dens m>0
0.0700 mer force
0.0700 potl
0.0700 potl m=0
0.0700 potl m>0
0.0700 rad force
----------------------------------------
0.0800 azi force
0.0800 dens
0.0800 dens m=0
0.0800 dens m>0
0.0800 mer force
0.0800 potl
0.0800 potl m=0
0.0800 potl m>0
0.0800 rad force
----------------------------------------
0.0900 azi force
0.0900 dens
0.0900 dens m=0
0.0900 dens m>0
0.0900 mer force
0.0900 potl
0.0900 potl m=0
0.0900 potl m>0
0.0900 rad force
----------------------------------------
0.1000 azi force
0.1000 dens
0.1000 dens m=0
0.1000 dens m>0
0.1000 mer force
0.1000 potl
0.1000 potl m=0
0.1000 potl m>0
0.1000 rad force
----------------------------------------
0.1100 azi force
0.1100 dens
0.1100 dens m=0
0.1100 dens m>0
0.1100 mer force
0.1100 potl
0.1100 potl m=0
0.1100 potl m>0
0.1100 rad force
----------------------------------------
0.1200 azi force
0.1200 dens
0.1200 dens m=0
0.1200 dens m>0
0.1200 mer force
0.1200 potl
0.1200 potl m=0
0.1200 potl m>0
0.1200 rad force
----------------------------------------
0.1300 azi force
0.1300 dens
0.1300 dens m=0
0.1300 dens m>0
0.1300 mer force
0.1300 potl
0.1300 potl m=0
0.1300 potl m>0
0.1300 rad force
----------------------------------------
0.1400 azi force
0.1400 dens
0.1400 dens m=0
0.1400 dens m>0
0.1400 mer force
0.1400 potl
0.1400 potl m=0
0.1400 potl m>0
0.1400 rad force
----------------------------------------
0.1500 azi force
0.1500 dens
0.1500 dens m=0
0.1500 dens m>0
0.1500 mer force
0.1500 potl
0.1500 potl m=0
0.1500 potl m>0
0.1500 rad force
----------------------------------------
0.1600 azi force
0.1600 dens
0.1600 dens m=0
0.1600 dens m>0
0.1600 mer force
0.1600 potl
0.1600 potl m=0
0.1600 potl m>0
0.1600 rad force
----------------------------------------
0.1700 azi force
0.1700 dens
0.1700 dens m=0
0.1700 dens m>0
0.1700 mer force
0.1700 potl
0.1700 potl m=0
0.1700 potl m>0
0.1700 rad force
----------------------------------------
0.1800 azi force
0.1800 dens
0.1800 dens m=0
0.1800 dens m>0
0.1800 mer force
0.1800 potl
0.1800 potl m=0
0.1800 potl m>0
0.1800 rad force
----------------------------------------
0.1900 azi force
0.1900 dens
0.1900 dens m=0
0.1900 dens m>0
0.1900 mer force
0.1900 potl
0.1900 potl m=0
0.1900 potl m>0
0.1900 rad force
----------------------------------------
0.2000 azi force
0.2000 dens
0.2000 dens m=0
0.2000 dens m>0
0.2000 mer force
0.2000 potl
0.2000 potl m=0
0.2000 potl m>0
0.2000 rad force
Using a point mesh instead of a grid
The FieldGenerator allows you to specify an array of Cartesian points for field evaluation. This way, you can get creative with geometries and mesh spacing. As an illustration, let us repeat the same renderings using this mesh-point method.
As a sanity check, let’s do the same plots as the grid example above.
[5]:
# First, we generate a Cartesian mesh
xy = np.linspace(-1, 1, 40)
mesh = np.ndarray((40*40, 3))
for i in range(40):
for j in range(40):
mesh[i*40+j, 0] = xy[i]
mesh[i*40+j, 1] = xy[j]
mesh[i*40+j, 2] = 0.0
Now that we have the a point set, in a Cartesian grid for this test, generate the points:
[6]:
fields = pyEXP.field.FieldGenerator(times, mesh)
points = fields.points(basis, coefs)
# Print the potential image at the final time (I think there is a
# fencepost issue in this grid, no matter).
x = np.linspace(pmin[0], pmax[0], grid[0])
y = np.linspace(pmin[1], pmax[1], grid[1])
xv, yv = np.meshgrid(x, y)
def tomesh(points):
ret = np.zeros(xv.shape)
print(ret.shape)
for i in range(40):
for j in range(40):
ret[i, j] = points[i*40+j]
return ret
# Visualize the final time slice in grid. Obviously, we could use any
# field we want. Here is potential and radial force.
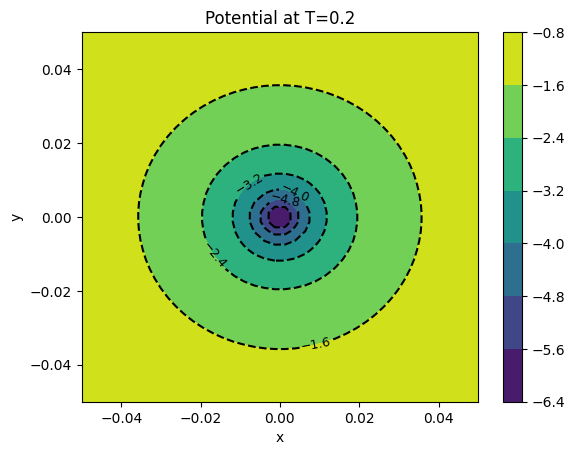
img = tomesh(points[final]['potl'])
cont1 = plt.contour(xv, yv, img, colors='k')
plt.clabel(cont1, fontsize=9, inline=True)
cont2 = plt.contourf(xv, yv, img)
plt.colorbar(cont2)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Potential at T={}'.format(final))
plt.show()
img = tomesh(points[final]['rad force'])
cont1 = plt.contour(xv, yv, img, colors='k')
plt.clabel(cont1, fontsize=9, inline=True)
cont2 = plt.contourf(xv, yv, img)
plt.colorbar(cont2)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Radial force at T={}'.format(final))
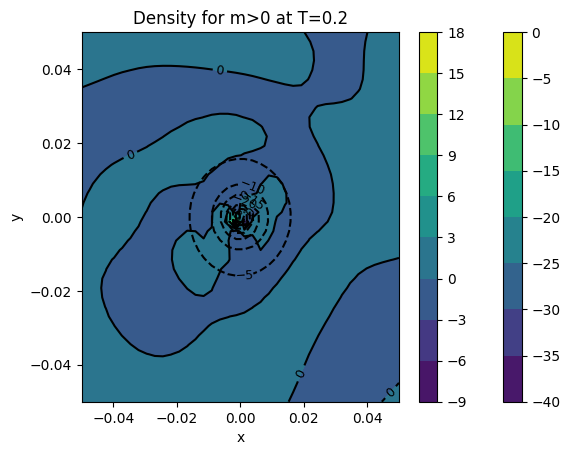
img = tomesh(points[final]['dens m>0'])
cont1 = plt.contour(xv, yv, img, colors='k')
plt.clabel(cont1, fontsize=9, inline=True)
cont2 = plt.contourf(xv, yv, img)
plt.colorbar(cont2)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Density for m>0 at T={}'.format(final))
(40, 40)
(40, 40)
(40, 40)
[6]:
Text(0.5, 1.0, 'Density for m>0 at T=0.2')
Now, let’s take advantage of the unstructured point set for something different
First, let’s make a point set on a spherical surface:
[7]:
# First, we generate a Cartesian mesh
phi = np.linspace(0.0, 2.0*math.pi, 40)
cost = np.linspace(-1.0, 1.0, 40)
mesh = np.ndarray((40*40, 3))
radius = 1.0
for i in range(40):
for j in range(40):
sint = np.sqrt(1.0 - cost[j]**2)
mesh[i*40+j, 0] = radius*sint*math.cos(phi[i])
mesh[i*40+j, 1] = radius*sint*math.sin(phi[i])
mesh[i*40+j, 2] = radius*cost[j]
Generate a new point set for this unstructured grid as follows:
[8]:
fields = pyEXP.field.FieldGenerator(times, mesh)
points = fields.points(basis, coefs)
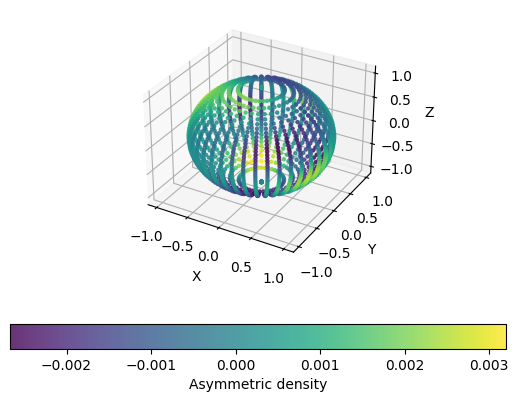
Now, let’s make a 3d scatter plot with points colored by field values:
[9]:
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
sc = ax.scatter(mesh[:,0], mesh[:,1], mesh[:,2], c=points[times[-1]]['dens m>0'], marker='o', s=5, alpha=0.8)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.colorbar(sc, label='Asymmetric density', orientation='horizontal')
plt.show()
Using MSSA
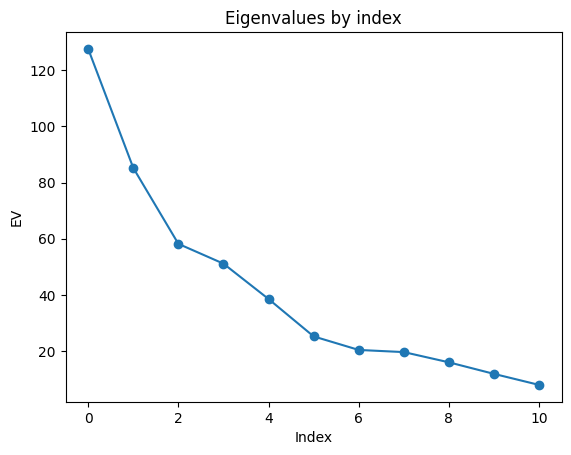
Generate the initial MSSA analyis and plot the run of eigenvalues
[10]:
# Make a subkey sequence
#
keylst = coefs.makeKeys([2])
print("Keys=", keylst)
name = 'dark halo'
config = {name: (coefs, keylst, [])}
# This is the window length. The largest meaningful length is half
# the size of the time series. We'll choose that here but it *is*
# interesting to retry these analyses with different window lengths.
window = int(len(coefs.Times())/2)
npc = 10
print("Window={} PC number={}".format(window, npc))
ssa = pyEXP.mssa.expMSSA(config, window, npc)
ev = ssa.eigenvalues()
plt.plot(ev, 'o-')
plt.xlabel("Index")
plt.ylabel("EV")
plt.title("Eigenvalues by index")
plt.show()
Keys= [[2, 0, 0], [2, 0, 1], [2, 0, 2], [2, 0, 3], [2, 0, 4], [2, 0, 5], [2, 0, 6], [2, 0, 7], [2, 0, 8], [2, 0, 9], [2, 1, 0], [2, 1, 1], [2, 1, 2], [2, 1, 3], [2, 1, 4], [2, 1, 5], [2, 1, 6], [2, 1, 7], [2, 1, 8], [2, 1, 9], [2, 2, 0], [2, 2, 1], [2, 2, 2], [2, 2, 3], [2, 2, 4], [2, 2, 5], [2, 2, 6], [2, 2, 7], [2, 2, 8], [2, 2, 9]]
Window=10 PC number=10
---- Eigen is using 4 threads
shape U = 500 x 11
shape Y = 11 x 500
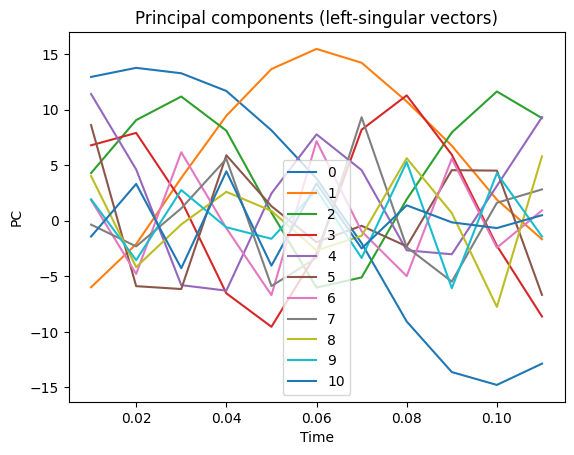
Next plot the principle components.
[11]:
times = coefs.Times();
pc = ssa.getPC();
rows, cols = pc.shape
for i in range(cols):
plt.plot(times[0:rows], pc[:,i], '-', label="{:d}".format(i))
plt.xlabel('Time')
plt.ylabel('PC')
plt.legend()
plt.title("Principal components (left-singular vectors)")
plt.show()
Now try a reconstruction
[12]:
coefs.zerodata() # <---replace with reconstructed
ssa.reconstruct([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
newdata = ssa.getReconstructed()
print('newdata is a', type(newdata))
newdata is a <class 'dict'>
Compute the k-means analysis
The k-means partitions n vector observations into k clusters in which each observation belongs to the cluster with the nearest centers while minimizing the variance within each cluster. In this case, the vectors are the full trajectory matrices and the distance is the distance between the trajectory matricies reconstructed from each eigentriple from mSSA. The distance used here is the Frobenius distance or matrix norm distance: the square root of the sum of squares of all elements in the difference between two matrices.
Note: the k-means analysis will use the reconstructions from your last call to reconstruct. In this notebook, that would be from the previous cell; the first 10 PCs. The k-means initial cluster selection chooses every second PC by default. This is a good choice for time series representing quasi-periodic motion which generally have pairs of PCs representing the sinusoidal behavior.
The k-means analysis illustrates the clear patterns in the PCs seen in the plots above: the individual features occur in pairs, dominated by the first two pairs as seen in the eigenvalue plot. This dominant pair is assigned id=0. The next pair is assigned id=1. The rest of the PCs are not particularly correlated and are lumped into id=0.
[13]:
# Print k-means groups, allowing up to 6
#
id, dist, tol = ssa.kmeans(clusters=6)
# Print the results
print('{:<4s} | {:<4s} | {:<13s}'.format('PC', 'id', 'distance'))
print('{:<4s} | {:<4s} | {:<13s}'.format('----', '----', '--------'))
for k in range(len(id)):
print('{:<4d} | {:<4d} | {:<13.6e}'.format(k, id[k], dist[k]))
PC | id | distance
---- | ---- | --------
0 | 0 | 6.243771e+00
1 | 0 | 6.243771e+00
2 | 1 | 4.312612e+00
3 | 1 | 4.312612e+00
4 | 2 | 0.000000e+00
5 | 3 | 2.561358e+00
6 | 3 | 2.561358e+00
7 | 4 | 2.330193e+00
8 | 4 | 2.342835e+00
9 | 4 | 2.861371e+00
In this case, k-means identifies 5 groups: 3 pairs and triple. Compare this with the results from the w-correlation matrix in the next section…
You can see from the PCs themselves, that very few dynamical periods are available for analysis. This simulation is not long enough for a highly signficant cluster analysis.
Finally plot the w-correlation matrix
This is the sum of the w-correlation matrices for all channels.
[14]:
mat = ssa.wCorrAll()
x = plt.pcolormesh(mat)
plt.title("All channels")
plt.colorbar(x)
plt.show()
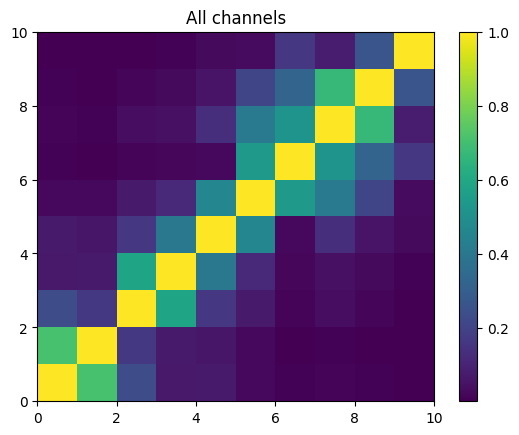
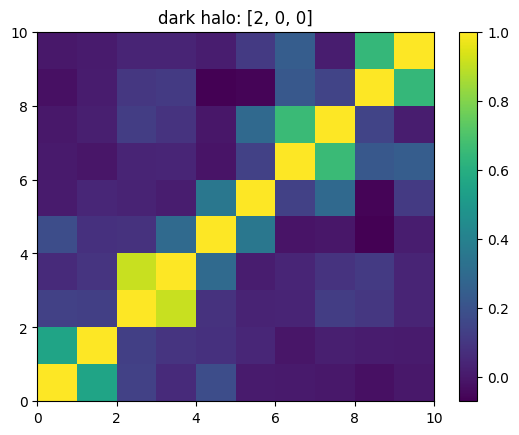
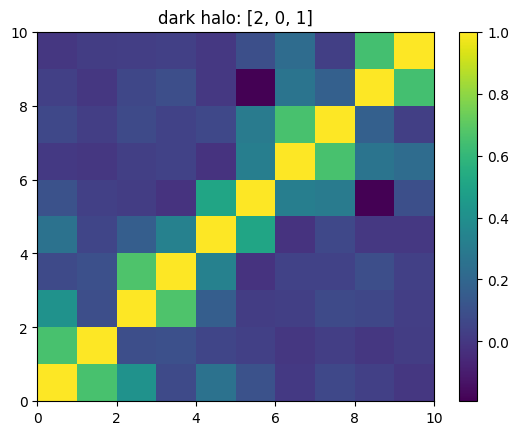
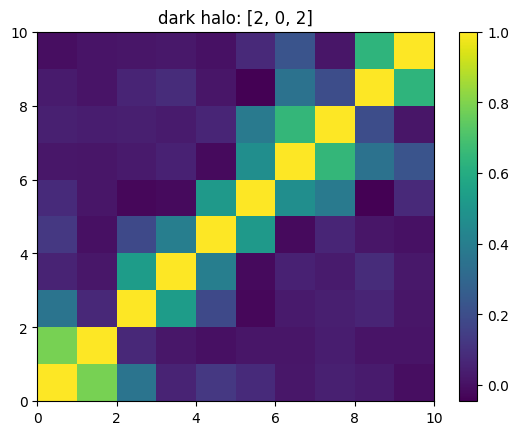
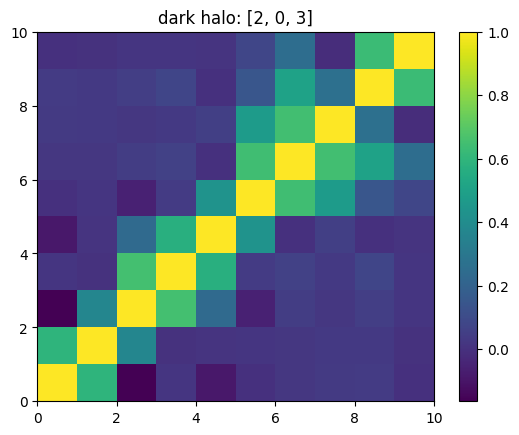
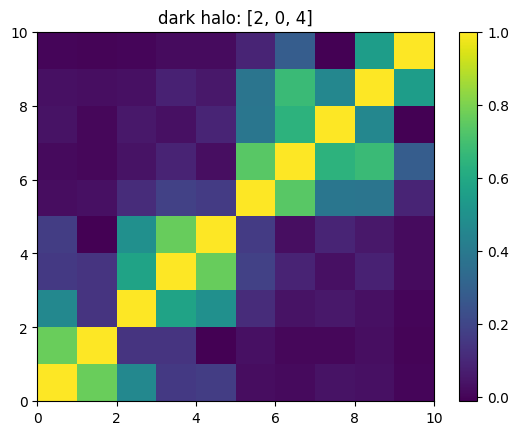
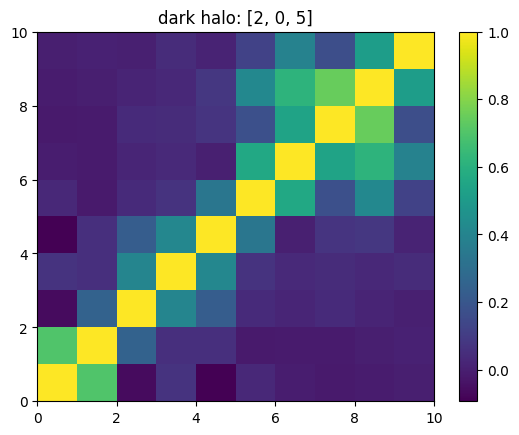
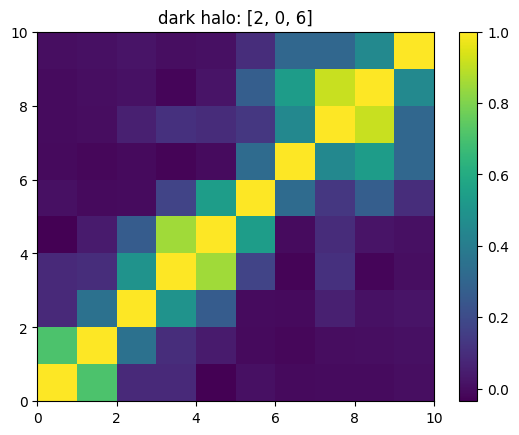
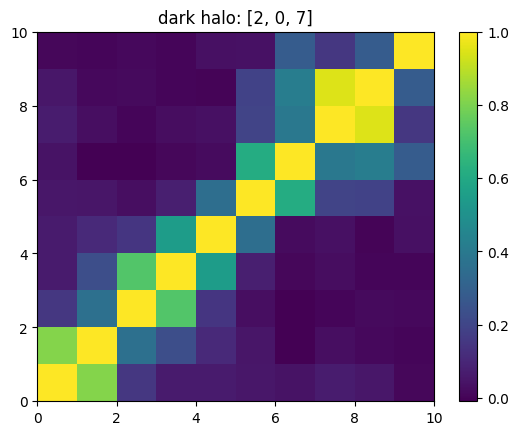
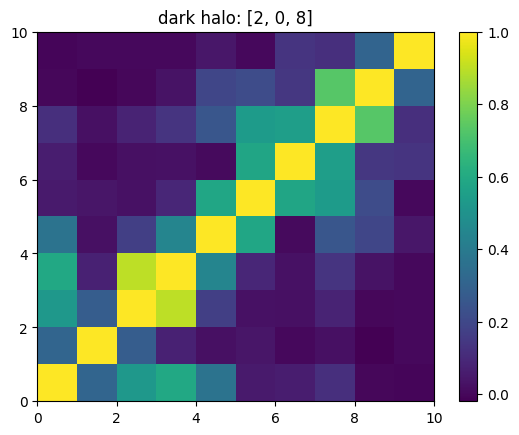
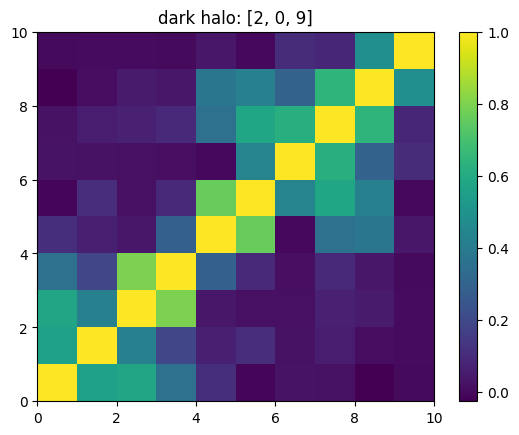
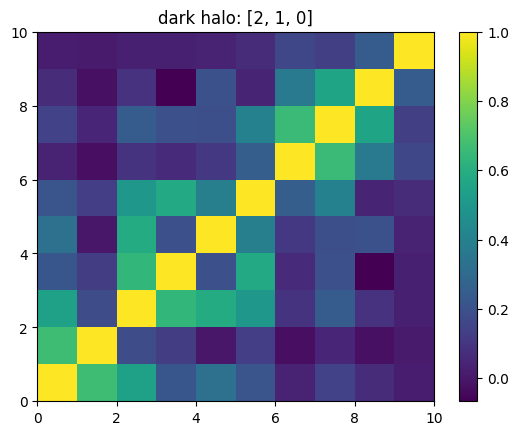
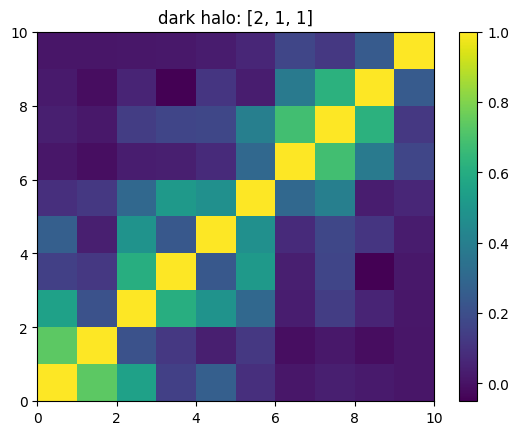
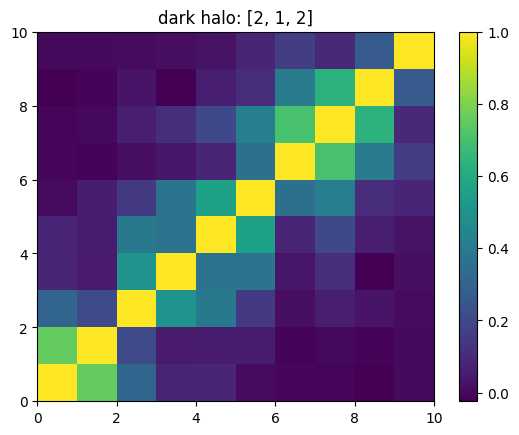
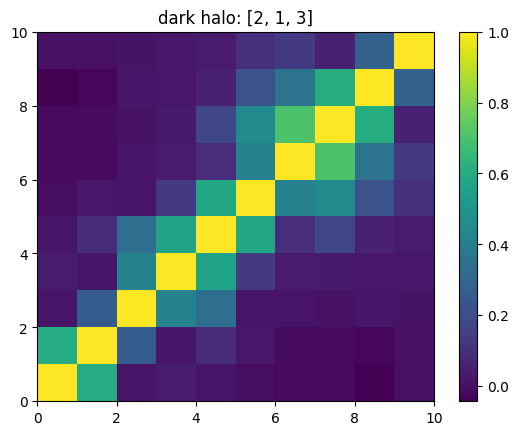
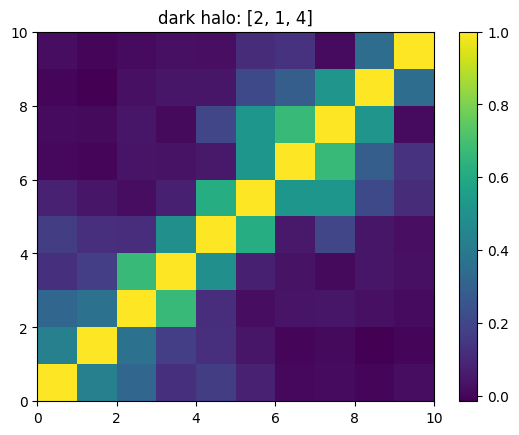
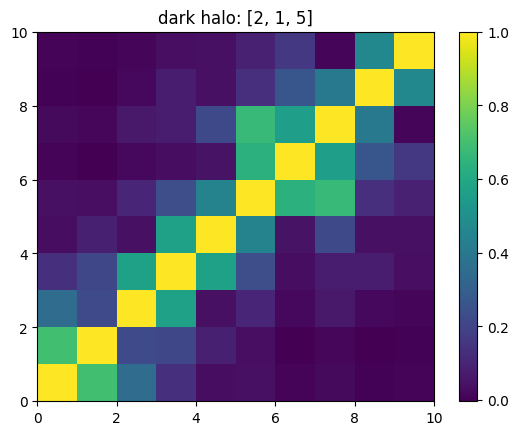
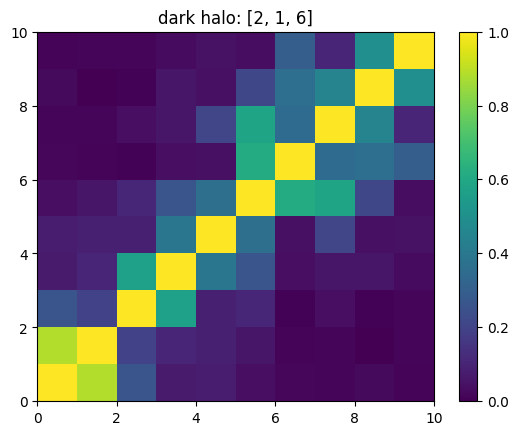
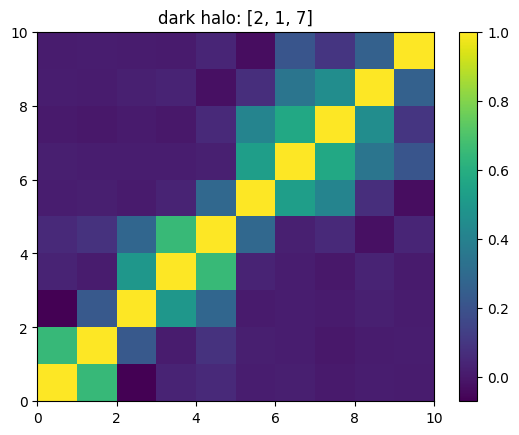
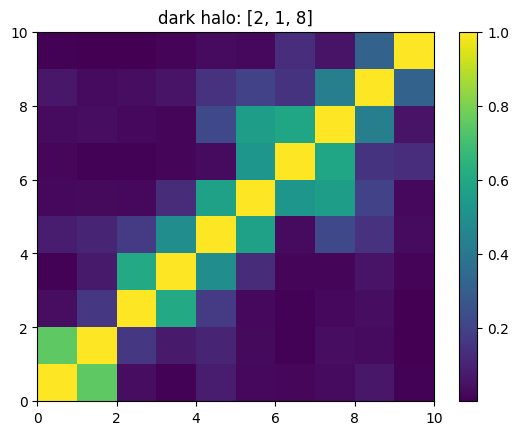
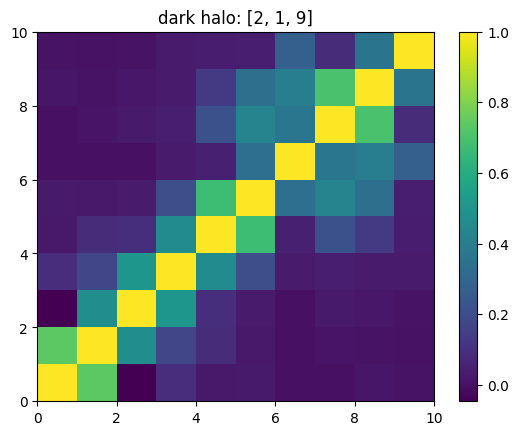
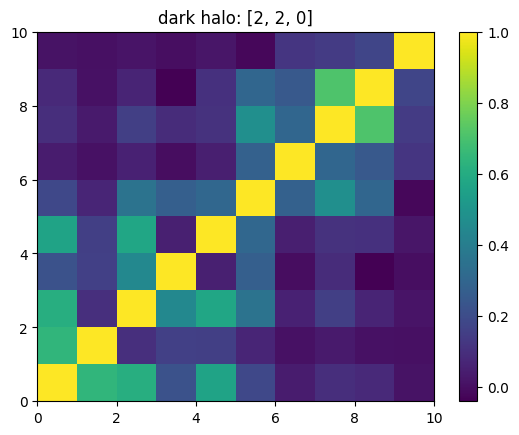
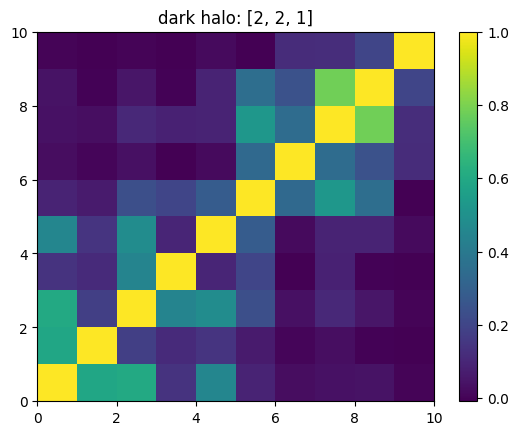
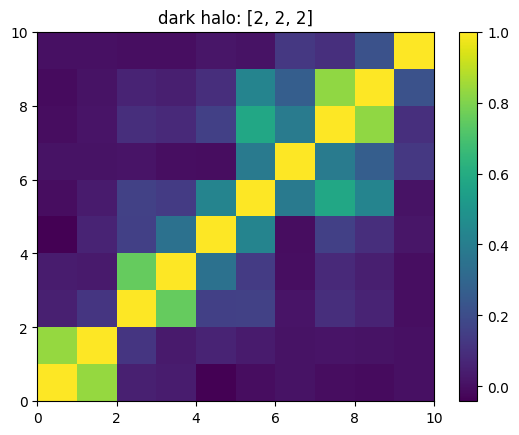
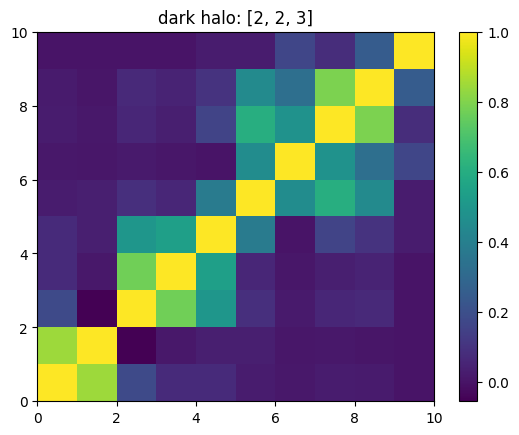
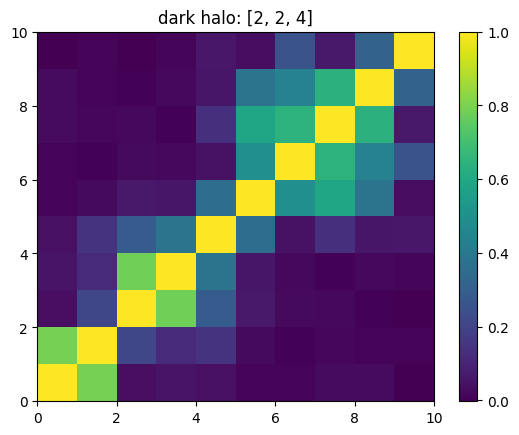
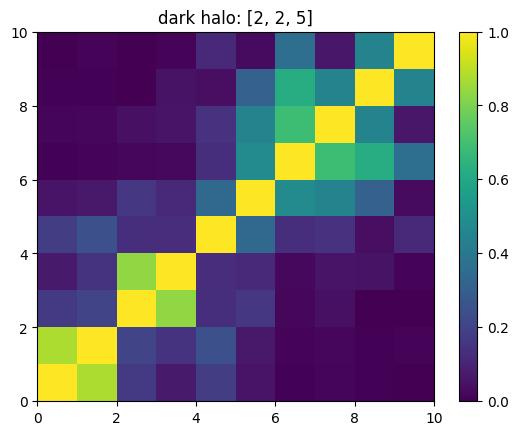
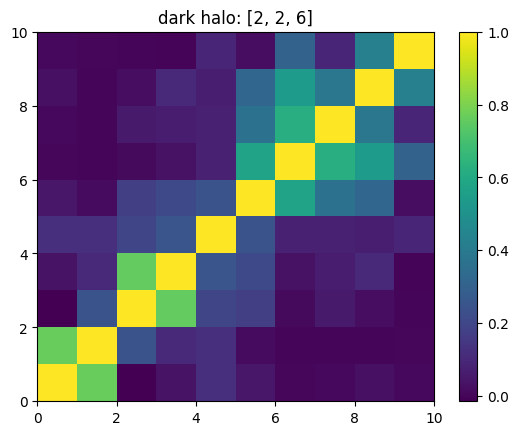
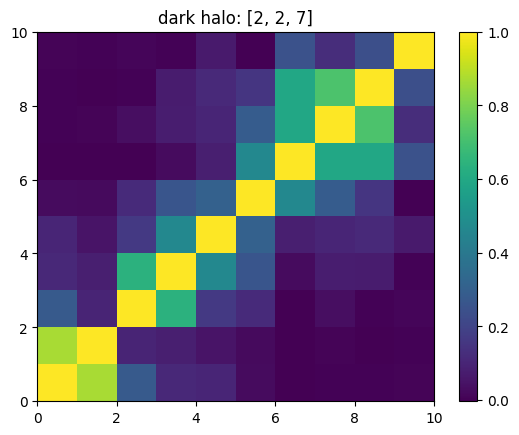
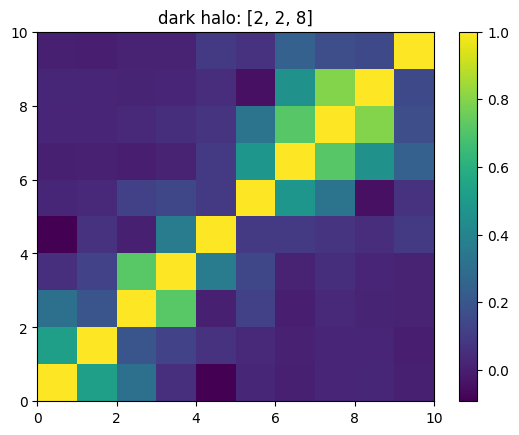
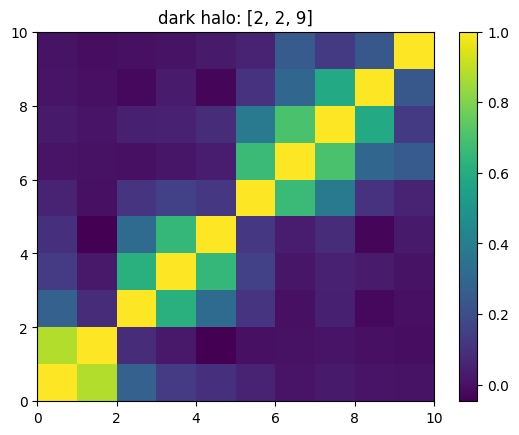
One can also look at individual channels.
[15]:
# Get and view the w-correlation matrices
# for each key individually
#
for k in keylst:
mat = ssa.wCorr(name, k)
# Plot it
x = plt.pcolormesh(mat)
plt.title('{}: {}'.format(name,k))
plt.colorbar(x)
plt.show()